前言
Splay其实并不是一种数据结构,而是给另一种数据结构进行优化的方式。
预备
Splay是建立在二叉查找树(BST)的基础上的,所以要学会Splay,就必须先了解二叉查找树。二叉查找树的形态是一颗形如这样的二叉树:
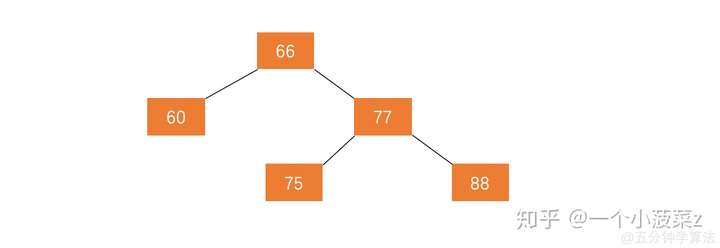
具体查找操作看OI-Wiki,大致操作就是和当前子树的根节点的val值进行比较,若大于,则往又查找;若小于,则往左查找。这样的话,我们在进行中序遍历的时候呈现出来的val值就是一个递增的序列,看图:

至于插入与删除,真是一眼难尽,还是老老实实去wiki上看吧。
正文
Why Splay?
在预备中我们讲到了,二叉查找树。但是,为什么要用到他呢?因为她
省时间还不占空间
唯一的槽点就是码量巨TM大,这也是为什么在实际比赛中用不到它,在做一般的题目时有种杀鸡用牛刀的感觉。我线段树它不香么。那么,由于使用的是二叉树,时间复杂度就可以降到log级别。燃鹅,真的是这样么?在经历几次插入的折磨后,我们的二叉树可能就会变成这样:
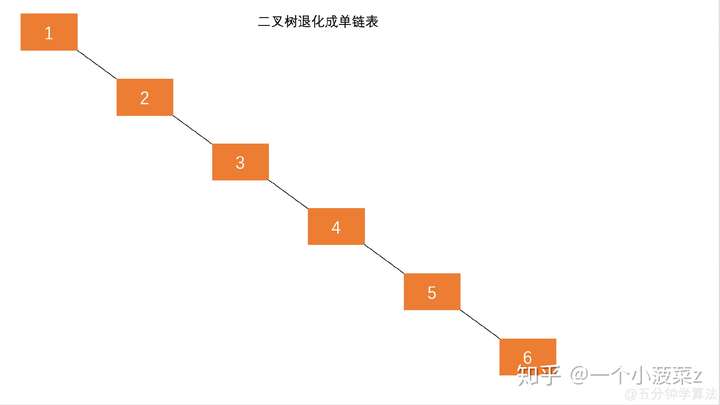
没错,这也是一颗二叉树。但是退化成这样之后,时间又变成O(n)了。。。
SH*TTTTTTTTTTTTTT
这时候,我们可以通过一种方法叫做“旋转”来重新使这棵树平衡,而旋转也是二叉树的基本操作。
旋转
Warning:接下来的内容可能需要几分钟。

旋转分为两种,一种看图:

(别问我为什么是图不在中间,鬼知道Microsoft WhiteBoard她是怎么排版的)
什么,你说你搞不懂?那我们一步一步来剖析:
注意,这只是帮助你理解如何旋转,在程序中无需体现也无法体现
Step 1

Step 2

Step 3

return 0;
这种旋转被称之为右旋,而左旋与之完全镜像,如图:

(好像我挪一挪位置这个图又到中间来了)
验证
那么,这样子会不会对原图有修改呢?有,肯定有,你看C节点很明显被提上来一层(dep[c]++)。但是,这样旋转对中序遍历又没有影响,我们举例说明:

看,没有影响!
我们先翻译成中文,右旋的步骤就是:
- C点的爸爸改为A
- B点的爸爸改为C
- A点的左儿子改为C
- B点的左儿子改为2,即C点原来的右儿子
- C点的右儿子改为B
我们称这一过程为rotate,代码在下面:
void rotate(int x)
{//0为左儿子;1为右儿子
int a=t[t[x].fa].fa;
int b=t[x].fa;
int c=x;
t[a].ch[0]=c;
t[b].ch[0]=t[c].ch[1];
t[c].ch[1]=b;
t[c].fa=a;
t[b].fa=c;
return;
}
这是右旋,那么左旋我们需要专门写一个函数么?不要,不要,千万不要,如果又写函数,Splay哪有美好的未来?哪有美好的前程?平衡树哪有栋梁之材?
前面我们说过,左旋与右旋是完全相反的,即左旋的步骤是这样的:
- C点的爸爸改为A
- B点的爸爸改为C
- A点的右儿子改为C
- B点的右儿子改为2,即C点原来的左儿子
- C点的左儿子改为B
所以,我们可以这样写:
void rotate(int x)
{//0为左儿子;1为右儿子
int a=t[t[x].fa].fa;
int b=t[x].fa;
int c=x;
int opt;
if (t[c].val<t[b].val) opt=0;//右旋
else opt=1;//左旋
t[a].ch[opt]=c;
t[b].ch[opt]=t[c].ch[1-opt];
t[c].ch[1-opt]=b;
t[c].fa=a;
t[b].fa=c;
return;
}
或者高级一点,把if去掉
void rotate(int x)
{//0为左儿子;1为右儿子
int a=t[t[x].fa].fa;
int b=t[x].fa;
int c=x;
int opt=t[c].val>t[b].val;
t[c].fa=a;
t[b].fa=b;
t[a].ch[opt]=c;
t[b].ch[opt]=t[c].ch[1-opt];
t[c].ch[1-opt]=b;
return;
}
那么,这就是我们旋转步骤了。
return 0;
Splay
Splay的精髓就在于如何旋转。如图:

+ 如果x的父亲是根节点,直接将 左旋或右旋(图1、2)。
+ 如果x的父亲不是根节点,且x和父亲的儿子类型相同,首先将其父亲左旋或右旋,然后将 x右旋或左旋(图3、4)。
+ 如果x的父亲不是根节点,且x和父亲的儿子类型不同,将x左旋再右旋、或者右旋再左旋(图5、6)。
所谓类型,即一个节点是其父亲的左/右儿子。
使用
那么,我们什么时候Splay?看代码吧:
P3369 【模板】普通平衡树
#include <bits/stdc++.h>
#define MAXN 500005
#define re register
using namespace std;
int root,tot;
struct node{
int ch[2];
int ff;
int cnt;
int val;
int son;
};
node edge[MAXN];
void push_up(int x)
{
edge[x].son=edge[edge[x].ch[0]].son+edge[edge[x].ch[1]].son+edge[x].cnt;
}
void rotate(int x)
{
re int y=edge[x].ff;
re int z=edge[y].ff;
re int k=edge[y].ch[1]==x;
edge[z].ch[edge[z].ch[1]==y]=x;
edge[x].ff=z;
edge[y].ch[k]=edge[x].ch[k^1];
edge[edge[x].ch[k^1]].ff=y;
edge[x].ch[k^1]=y;
edge[y].ff=x;
push_up(y);
push_up(x);
}
void splay(int x,int goal)
{
while (edge[x].ff!=goal)
{
int y=edge[x].ff;
int z=edge[y].ff;
if (z!=goal)
(edge[y].ch[0]==x)^(edge[z].ch[0]==y)?rotate(x):rotate(y);
rotate(x);
}
if (!goal) root=x;
}
void ins(int x)
{
int u=root;
int ff=0;
while (u && edge[u].val!=x)
{
ff=u;
u=edge[u].ch[x>edge[u].val];
// cout<<"asda"<<endl;
}
if (u) edge[u].cnt++;
else
{
tot++;
u=tot;
if (ff) edge[ff].ch[x>edge[ff].val]=u;
edge[tot].ch[0]=edge[tot].ch[1]=0;
edge[tot].ff=ff;
edge[tot].val=x;
edge[tot].cnt=edge[tot].son=1;
}
splay(u,0);
}
void find(int x)
{
int u=root;
if (!u) return;
while (edge[u].ch[x>edge[u].val] && x!=edge[u].val)
u=edge[u].ch[x>edge[u].val];
splay(u,0);
}
int nex(int x,int f)
{
find(x);
int u=root;
if ((edge[u].val>x && f) || (edge[u].val<x && !f))
return u;
u=edge[u].ch[f];
while (edge[u].ch[f^1])
u=edge[u].ch[f^1];
return u;
}
void del(int x)
{
int la=nex(x,0);
int ne=nex(x,1);
splay(la,0);
splay(ne,la);
int de=edge[ne].ch[0];
if (edge[de].cnt>1)
{
edge[de].cnt--;
splay(de,0);
}
else edge[ne].ch[0]=0;
}
int kth(int x)
{
int u=root;
if (edge[u].son<x)
return 0;
while (true)
{
int y=edge[u].ch[0];
if (x>edge[y].son+edge[u].cnt)
{
x-=edge[y].son+edge[u].cnt;
u=edge[u].ch[1];
}
else if (edge[y].son>=x) u=y;
else return edge[u].val;
// cout<<u<<" "<<y<<" "<<x<<endl;
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
// freopen("in.in","r",stdin);
// cout<<"asd"<<endl;
ins(INT_MAX);
ins(INT_MAX*-1);
int q;
cin>>q;
// cout<<"fhnasfkjg"<<endl;
for (int i=1;i<=q;i++)
{
int opt,tmp;
cin>>opt>>tmp;
// cout<<opt<<" "<<tmp<<endl;
switch(opt)
{
case 1:ins(tmp);break;
case 2:del(tmp);break;
case 3:find(tmp);cout<<edge[edge[root].ch[0]].son<<endl;break;
case 4:cout<<kth(tmp+1)<<endl;break;
case 5:cout<<edge[nex(tmp,0)].val<<endl;break;
case 6:cout<<edge[nex(tmp,1)].val<<endl;break;
}
// cout<<opt<<" "<<tmp<<endl;
}
return 0;
}
码量巨大。。。
总结
Splay是一个很优秀的算法,它能够很好地对平衡树进行动态调整,能在log级别的时间下完成插入,查询,修改及许多区间操作。但是,相比线段树,Splay,或者说平衡树,的码量太过庞大,且细节很多,不易检查,所以在真正比赛时我们能用线段树绝不用平衡树。
维护平衡树还有其它许多算法,例如不用旋转的Treap,这个算法可以实现平衡树的可持久化,不过我们后面再说吧
是我太菜了。
GB。
发表回复